
Магнитные Бури
Отслеживайте геомагнитные колебания в режиме реального времени. Несколько графиков с постоянным обновлением. Визуализация вспышек на Солнце, прогноз магнитных бурь на несколько дней вперед. Достоверная информация из проверенных источников (NASA, swpc.noaa.gov, space.umd.edu, iswa.gsfc.nasa.gov)

Землетрясения
Карта подземных толчков, которая обновляется в режиме реального времени. Мониторинг землетрясений с точным указанием очага, магнитуды, времени.

Солнце
Снимки нашей звезды со спутников NASA. Следите за Солнцем онлайн, изучайте его поведение, наблюдайте за вспышками, которые приводят к магнитным бурям. Фотографии получены из проверенных источников и мониторинг происходит в режиме реального времени.

Луна
Следите за фазами луны вместе с нами. Снимки месяца регулярно обновляются, фотографии поступают из двух проверенных источников. Не нужно выходить на улицу в поисках Луны. Какой месяц сегодня, узнайте на этой странице прямо сейчас.
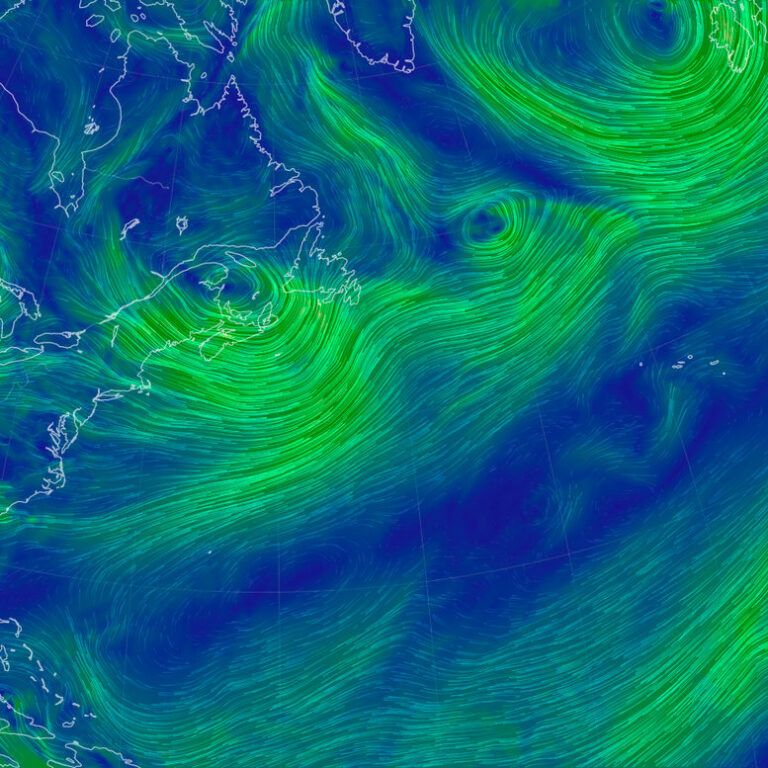
Ветры
Карта направления ветров, куда дует и с какой силой, какая скорость ветра. Удобный интуитивно понятный интерфейс сервиса, который предоставляет онлайн все необходимые данные о воздушных массах по планете.

Полеты
Карта полетов самолетов от всемирно известного сервиса. Марки бортов, время вылета и прибытия, фото и много другой полезной информации. Полезный инструмент, который также работает онлайн, стабильно, без выходных и перерывов на обед.

Радиация
Онлайн мониторинг радиационного фона. Карта с автоматическим обновлением, регулярное поступление свежих данных из множества наземных станций. Радиация не пройдет!

Тайфуны, ураганы
Карта штормов, ураганов и тайфунов, на которой в режиме онлайн отслеживается состояние нашей атмосферы на предмет появления мощных природных катаклизмов, связанных с сильным ветром и осадками.
Следите за событиями в мире не выходя из дома
Трекинг в режиме реального времени мгновенно предоставляет информацию по конкретному запросу. Автоматическое обновление всех существующих на нашем сайте мониторов позволяет получать актуальные данные с самых дальних уголков планеты.
Пожары, происшествия, крушения самолетов, геомагнитные волнения, стабильность радиосвязи и GPS, извержение вулканов, уровень загрязнения воздуха — все это и многое другое можно отслеживать, наблюдать, мониторить, анализировать, исследовать вместе с нами.
Мы работаем над расширением нашего диапазона покрытия, изучаем и ищем надежные источники онлайн карт, которые будут помогать нам следить за ситуацией на планете. Если вы не нашли какие-либо данные, сообщите нам и мы постараемся добавить это на сайт как можно быстрей.
Совсем скоро вы сможете в режиме реального времени осуществлять мониторинг воздуха, судов, рейсов самолетов и кораблей, пожаров на планете, наблюдать онлайн происшествия с указанием точного времени и локации на карте.